La Stratégie de l\'Appât

Nombre d'or

Texte extrait de l'encyclopédie Wikipédia

Le nombre d'or est la proportion, définie initialement en géométrie, comme l'unique rapport entre deux longueurs telles que le rapport de la somme des deux longueurs (a+b) sur la plus grande (a) soit égal à celui de la plus grande (a) sur la plus petite (b) c'est à dire lorsque (a+b)/a = a/b. Le découpage d'un segment en deux longueurs vérifiant cette propriété est appelée par Euclide découpage en extrême et moyenne raison. Le nombre d'or est maintenant souvent désigné par la lettre φ (phi) en l'honneur du sculpteur Phidias qui l'aurait utilisé pour concevoir le Parthénon.

Ce nombre irrationnel est l'unique solution positive de l'équation x² = x + 1.

Il vaut approximativement 1,618 033 989. Il intervient dans la construction du pentagone régulier et du rectangle d'or. Ses propriétés algébriques le lient à la suite de Fibonacci et permettent de définir une arithmétique du nombre d'or source de nombreuses démonstrations.

Rectangle d'or

Les calculs précédents permettent, à l'aide d'une règle et d'un compas de dessiner une proportion d'extrême et de moyenne raison. La méthode est illustrée sur la figure de gauche. On dessine un cercle de centre C et de rayon 1 (en orange). Puis, de l'extrémité du rayon, on élève un segment (en vert) perpendiculaire au rayon, de longueur 1/2, et on trace le cercle de centre C' et de rayon 1/2. Le segment bleu qui a pour extrémités C et le point du cercle C' dans le prolongement de CC'  est de longueur φ.

  Rectangles d'or et divine proportion

Cette méthode permet aussi de construire un rectangle d'or, c'est-à-dire un rectangle de longueur a et de largeur b tel que a et b soient en proportion d'extrême et de moyenne raison. En d'autres termes, un rectangle est dit d'or si le rapport entre la longueur et la largeur est égal au nombre d'or.

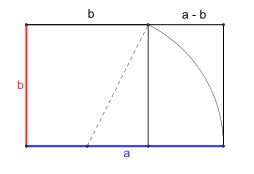
Pour tracer un rectangle d'or de longueur a et de largeur b, le plus simple est de dessiner un carré de côté b. En prenant le milieu de la base comme centre, on trace un cercle passant par les deux sommets opposés. L'intersection de la droite prolongeant la base du carré et du cercle détermine l'extrémité de la base du rectangle d'or. Il apparait comme construit par l'adjonction à un carré de côté de longueur b, d'un rectangle de côtés de longueur b et a - b, comme le montre la figure de droite.

Pentagone et pentagramme

Une fois la proportion d'extrême et de moyenne raison construite, il est simple de dessiner un pentagone.

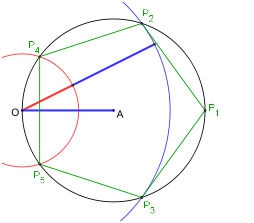
Un pentagone se construit à l'aide de la proportion d'extrême et moyenne raison. Soit un cercle de diamètre OP₁ et de rayon a, illustré sur la figure de gauche. Si b est le nombre réel plus petit que a tel que a et b soit en proportion d'or, et P₂, P₃, P₄ et P₅ les intersections du cercle de diamètre OP₁ avec les deux cercles de centre O et de rayon a + b et b, alors les cinq points P_i définissent un pentagone.

                           

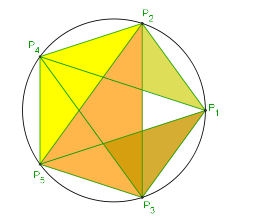
    Le pentagramme associé, c'est-à-dire la figure composée des cinq diagonales du pentagone, contient aussi de multiples proportions d'extrêmes et moyennes raisons. Elles s'expriment simplement à l'aide de triangles isocèles dont les longueurs des côtés sont en proportion d'or. De tels triangles sont appelés triangles d'or. Il en existe de deux types différents, les jaunes ayant une base proportionnelle à a et deux côtés à b et les orange ayant une base proportionnelle à b et deux côtés à a. Les triangles foncés sont semblables aux plus clairs de même couleur, la proportion entre clair et foncé est encore d'or.